三角形三个部分的知识整理、三角形的重心

三角形三个部分的知识整理、三角形的重心 ,对于想学习百科知识的朋友们来说，三角形三个部分的知识整理、三角形的重心是一个非常想了解的问题，下面小编就带领大家看看这个问题。

三角形的基本概念

三角形是平面几何中最基本的图形之一，由三条线段组成，它们相交于三个顶点。三角形的性质和特点在几何学中有着广泛的应用。下面将从三角形的定义、分类、内角和外角、边长关系以及面积等方面进行详细的阐述。

定义和分类

三角形是由三条线段组成的图形，它们相交于三个顶点。根据三条线段的长度关系，三角形可以分为三种类型：等边三角形、等腰三角形和一般三角形。等边三角形的三条边长度相等，等腰三角形的两条边长度相等，一般三角形的三条边长度各不相等。

内角和外角

三角形的内角和外角是三角形的重要性质。内角是指三角形内部的角度，三角形的内角和为180度。外角是指三角形的一个内角的补角，即等于180度减去该内角的度数。三角形的外角和等于360度。

边长关系

三角形的边长关系是三角形中的一个重要性质。根据三角形的边长关系，可以判断三角形的类型。三角形的任意两边之和大于第三边，任意两边之差小于第三边。根据这个关系，可以判断一个三角形是否存在。

面积

三角形的面积是三角形的另一个重要性质。三角形的面积可以通过三角形的底边和高来计算。三角形的底边为任意一边，高为从底边到对顶顶点的垂直距离。三角形的面积公式为：面积 = 底边长度 × 高 ÷ 2。

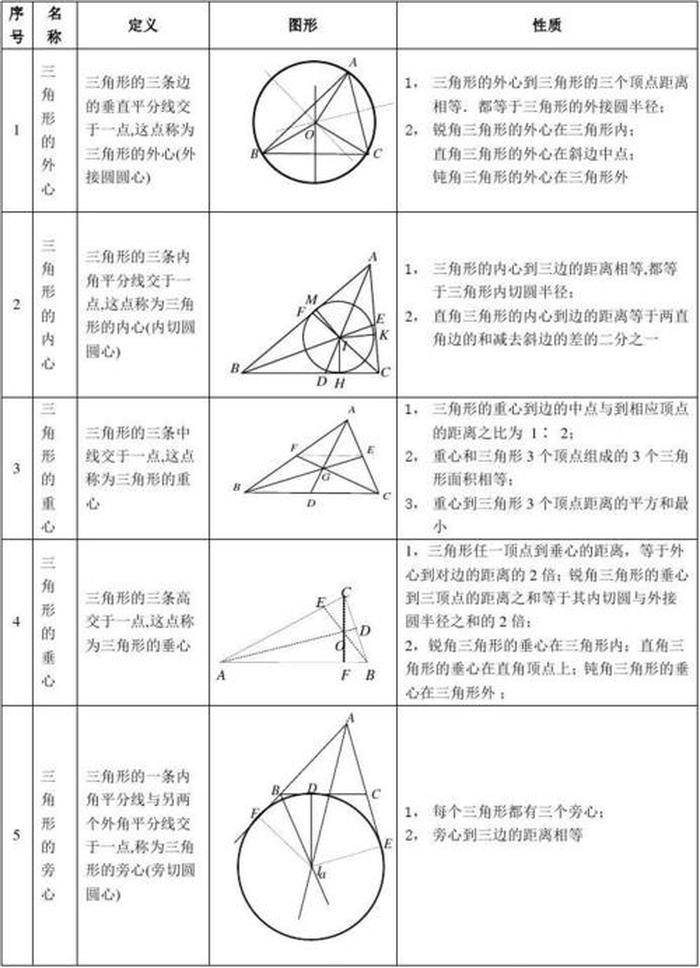
三角形的重心

三角形的重心是三角形内部的一个特殊点，它与三角形的三个顶点之间的距离相等。重心是三角形内部的一个重要点，它具有许多特殊性质和应用。

定义和性质

三角形的重心是三条中线的交点，中线是连接三角形的一个顶点和对边中点的线段。重心到三角形的三个顶点的距离相等，且重心到三角形的三条边的距离的和最小。重心将三角形分成三个面积相等的小三角形。

重心的坐标

三角形的重心的坐标可以通过三个顶点的坐标来计算。假设三角形的三个顶点分别为A(x1, y1)、B(x2, y2)和C(x3, y3)，则重心的坐标为：重心的x坐标 = (x1 + x2 + x3) ÷ 3，重心的y坐标 = (y1 + y2 + y3) ÷ 3。

重心的应用

重心在几何学中有着广泛的应用。重心可以用来确定三角形的形心，它是三角形内部的一个重要点。重心还可以用来确定三角形的质心，它是三角形内部的一个质量分布点。重心还可以用来确定三角形的中位线，它是连接三角形的一个顶点和对边中点的线段。

重心的计算方法

计算三角形的重心可以使用重心的坐标公式，也可以使用向量的方法。向量的方法是通过将三角形的三个顶点表示为向量，然后计算三个向量的和的1/3来得到重心的坐标。重心的计算方法可以根据具体的问题选择适合的方法。

三角形是平面几何中最基本的图形之一，具有许多重要的性质和特点。三角形的重心是三角形内部的一个特殊点，具有许多特殊性质和应用。了解三角形的基本概念和重心的性质对于几何学的学习和应用具有重要意义。

以上是关于三角形三个部分的知识整理、三角形的重心的介绍，希望对想学习百科知识的朋友们有所帮助。

本文标题：三角形三个部分的知识整理、三角形的重心；本文链接：http://yszs.weipeng.cc/zs/535294.html。