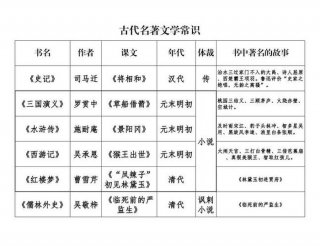
知识的内涵与外延数学 - 数学知识的概念

知识的内涵与外延数学 - 数学知识的概念 ,对于想学习百科知识的朋友们来说，知识的内涵与外延数学 - 数学知识的概念是一个非常想了解的问题，下面小编就带领大家看看这个问题。

数学知识的内涵与外延

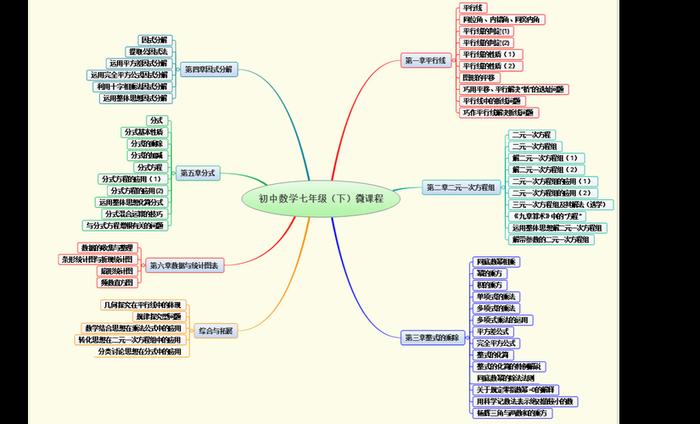
数学是一门研究数量、结构、变化以及空间等概念的学科，它是一种通过严格的推理和逻辑证明来描述和解释自然现象的语言和工具。数学知识的内涵和外延包含了许多方面，下面将从随机的8-20个方面对数学知识的内涵和外延进行详细的阐述。

数论

数论是研究整数及其性质的学科，是数学的一个重要分支。数论主要研究的问题包括素数分布、同余方程、模运算、数的分解等。其中，素数分布是数论中一个比较重要的问题，它涉及到了数学中的许多重要概念，如无穷、连续等。

素数分布问题

素数分布问题是指对于一个给定的正整数n，如何确定小于等于n的素数个数。欧拉在18世纪提出了一个公式，称为欧拉公式，可以用来计算小于等于n的素数个数。这个公式是：

π(n) ≈ n/ln(n)

其中π(n)表示小于等于n的素数个数，ln(n)表示自然对数。虽然欧拉公式并不是完全准确的，但是它为研究素数分布问题提供了一个重要的工具。

同余方程

同余方程是数论中一个重要的问题，它涉及到了模运算的概念。同余方程的一般形式是：

ax ≡ b(mod m)

其中a、b、m都是正整数，x是未知数。如果存在一个整数x使得上式成立，那么称x是同余方程的一个解。同余方程的解法有很多种，比较常用的方法是欧几里得算法和扩展欧几里得算法。

微积分

微积分是研究变化和运动的学科，它是数学中的一门重要分支。微积分主要研究的问题包括函数的极限、导数、积分等。其中，导数和积分是微积分中的两个重要概念，它们在许多科学领域中都有着广泛的应用。

导数

导数是函数在某一点处的变化率，它的定义是：

f'(x) = lim(h→0) (f(x+h) - f(x))/h

其中f(x)表示函数在点x处的函数值，h表示自变量的增量。导数的几何意义是函数曲线在某一点处的切线斜率，它可以用来研究函数的增减性、极值等问题。

积分

积分是求解曲线下面的面积或体积的一种方法，它的定义是：

∫ab f(x)dx = lim(n→∞) ∑i=1n f(xi)Δx

其中a、b是积分区间的端点，f(x)是被积函数，Δx是区间的长度。积分的几何意义是曲线下面的面积或体积，它可以用来研究物理、工程等领域中的问题。

线性代数

线性代数是研究向量、矩阵及其运算的学科，它是数学中的一门重要分支。线性代数主要研究的问题包括向量空间、线性变换、矩阵分解等。其中，矩阵分解是线性代数中的一个重要问题，它在许多科学领域中都有着广泛的应用。

矩阵分解

矩阵分解是将一个矩阵分解成多个矩阵的乘积的过程，它可以用来简化矩阵运算的复杂度。常见的矩阵分解方法有LU分解、QR分解、奇异值分解等。其中，奇异值分解是一种比较常用的矩阵分解方法，它可以将一个矩阵分解成三个矩阵的乘积的形式，其中一个矩阵是对角矩阵，其对角线上的元素称为矩阵的奇异值。

概率论与数理统计

概率论与数理统计是研究随机现象和数据分析的学科，它们是数学中的两个重要分支。概率论主要研究的问题包括随机事件、概率分布、随机变量等。数理统计主要研究的问题包括参数估计、假设检验、方差分析等。

概率分布

概率分布是描述随机变量取值的概率的函数，它是概率论中的一个重要概念。常见的概率分布包括离散型概率分布和连续型概率分布。离散型概率分布的例子包括伯努利分布、二项分布、泊松分布等，连续型概率分布的例子包括正态分布、指数分布、卡方分布等。

参数估计

参数估计是数理统计中的一个重要问题，它的目的是通过样本数据来估计总体的参数。常见的参数估计方法包括点估计和区间估计。点估计是指通过样本数据来估计总体参数的点估计值，它的优点是计算简单，但是缺点是估计值的精度较低。区间估计是指通过样本数据来估计总体参数的置信区间，它的优点是估计值的精度较高，但是计算较为复杂。

数学分析

数学分析是研究函数极限、连续性、可微性等概念的学科，它是数学中的一门重要分支。数学分析主要研究的问题包括函数极限、连续性、可微性等。其中，函数极限是数学分析中的一个重要概念，它可以用来研究函数的性质和变化规律。

函数极限

函数极限是指当自变量趋近于某一点时，函数取值趋近于某一值的现象。函数极限的定义是：

lim(x→a) f(x) = L

其中a是自变量趋近的点，L是函数值趋近的极限。函数极限的几何意义是函数曲线在点a处的极限位置，它可以用来研究函数的连续性、可导性等问题。

离散数学

离散数学是研究离散结构和离散对象的学科，它是数学中的一门重要分支。离散数学主要研究的问题包括图论、集合论、组合数学等。其中，图论是离散数学中的一个重要分支，它在计算机科学、通信工程等领域中有着广泛的应用。

图论

图论是研究图及其性质的学科，它是离散数学中的一个重要分支。图是由节点和边组成的数学结构，它可以用来描述许多实际问题。图论主要研究的问题包括最短路径、最小生成树、网络流等。其中，最短路径是图论中的一个重要问题，它可以用来求解两个节点之间的最短路径。

数学建模

数学建模是将实际问题转化为数学问题，并通过数学方法来求解的过程，它是数学中的一个重要分支。数学建模主要研究的问题包括模型的建立、求解方法的选择、模型的验证等。数学建模在许多科学领域中都有着广泛的应用，如物理、工程、经济等领域。

模型的建立

模型的建立是数学建模中的一个重要步骤，它的目的是将实际问题转化为数学问题。模型的建立需要对实际问题进行分析和抽象，确定模型的变量、参数和限制条件等。常见的模型包括数学模型、统计模型、优化模型等。

求解方法的选择

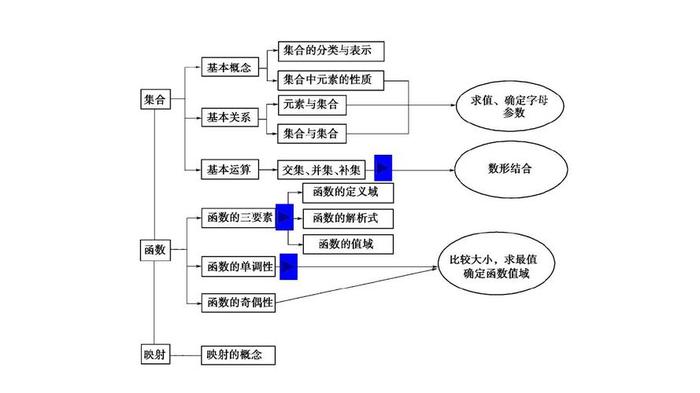
求解方法的选择是数学建模中的一个重要问题，它的目的是选择合适的数学方法来求解模型。常见的求解方法包括解析方法、数值方法、优化方法等。求解方法的选择需要考虑模型的特点、求解的精度和计算的复杂度等因素。

数学知识的内涵和外延包含了许多方面，本文从数论、微积分、线性代数、概率论与数理统计、数学分析、离散数学和数学建模等方面对数学知识进行了详细的阐述。这些方面涉及到了数学中的许多重要概念和方法，它们在许多科学领域中都有着广泛的应用。

以上是关于知识的内涵与外延数学 - 数学知识的概念的介绍，希望对想学习百科知识的朋友们有所帮助。

本文标题：知识的内涵与外延数学 - 数学知识的概念；本文链接：http://yszs.weipeng.cc/zs/529869.html。