数学建模从入门到精通、数学建模从入门到放弃

数学建模从入门到精通、数学建模从入门到放弃 ,对于想学习百科知识的朋友们来说，数学建模从入门到精通、数学建模从入门到放弃是一个非常想了解的问题，下面小编就带领大家看看这个问题。

引言：探索数字世界的神奇奥秘

随着科技的发展与创新，数学建模已逐渐融入我们的生活和工作之中。作为一门交叉性极强的学科，它犹如一条绚烂的星光大道，吸引无数热血青年前来探寻数字世界的神奇奥秘。入门容易，精通艰难。在这个复杂的学习过程中，你可能会遭遇困惑与挑战，产生放弃的念头。今天我们就一起聊聊这个话题，谈谈如何从数学建模的入门者逐步成为专家，以及如何克服挫折坚持走下去。但请别忘了，放弃也是一种智慧，有时候选择放弃是为了更好地前行。

一、初识数学建模：揭开神秘面纱

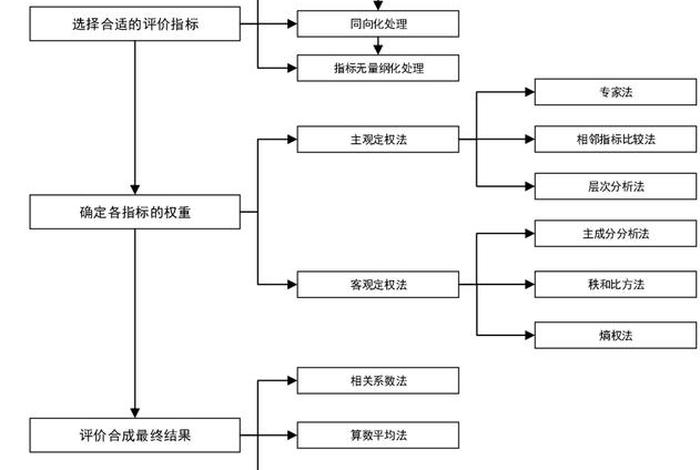
1. 数学建模的基本概念

数学建模是通过数学语言和方法对实际问题进行抽象描述的过程。从实际问题中提炼出数学模型，再通过计算机进行求解和验证。这是数学与实际应用相结合的一种重要方式。初学者可以从简单的线性模型入手，逐步深入了解非线性模型、动态模型等复杂概念。

2. 数学建模的应用领域

数学建模广泛应用于物理、化学、生物、经济、金融等多个领域。从物理学中的力学问题到金融市场的风险评估，从生物学中的生物信息学到环境保护中的数据处理，都能见到数学建模的影子。丰富多彩的实践背景有助于激发学习兴趣和动力。

二、进阶之路：从入门到精通

1. 掌握基础知识

要想在数学建模领域有所建树，首先要熟练掌握数学基础知识。线性代数、微积分、概率统计等是必备技能。还需要学习编程语言如Python或MATLAB进行数值计算。只有打好基础，才能在后续的学习中得心应手。

2. 实践锻炼

理论学习固然重要，但实践锻炼同样不可或缺。通过参加各类数学建模竞赛、参与科研项目或实习等方式，可以锻炼解决实际问题的能力。在实践中不断积累经验，将理论知识与实际需求紧密结合。

3. 持续学习

数学建模是一个不断学习和进步的过程。随着科技的发展，新的理论和方法不断涌现。要想保持竞争力，需要持续学习新知识，关注前沿动态，不断拓展自己的知识边界。通过参加研讨会、阅读专业文献、在线课程等方式，不断提升自己的专业素养。

三、遭遇挫折：从坚持到放弃的思考

1. 面对困难与挑战

在学习的过程中，每个人都会遇到困难和挑战。面对复杂的问题和繁琐的计算，可能会产生挫败感和焦虑情绪。这时需要调整心态，保持积极面对困难的态度。

2. 理性评估

当遇到难以克服的困难时，需要理性评估自己的能力和兴趣。有时候放弃也是一种智慧。选择放弃并不意味着失败，而是为了更好地调整方向，寻找更适合自己的发展道路。尝试接受新的知识和领域也许会带来新的机遇和发现。

当然如果您觉得这篇文章不够满足您的需求可以再继续写出更多的小标题供您参考：比如如何克服学习中的难点与瓶颈期；如何寻找合适的资源与支持；如何培养对数学建模的兴趣与热情等等都是值得探讨的话题和内容哦。

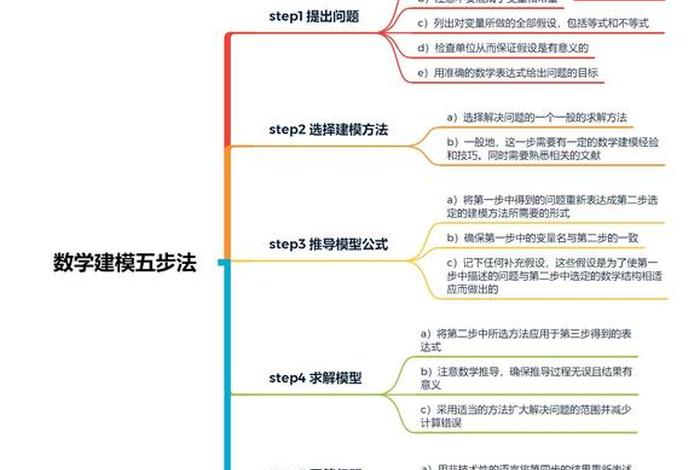
以上是关于数学建模从入门到精通、数学建模从入门到放弃的介绍，希望对想学习百科知识的朋友们有所帮助。

本文标题：数学建模从入门到精通、数学建模从入门到放弃；本文链接：http://yszs.weipeng.cchttp://yszs.weipeng.cc/xx/593513.html。